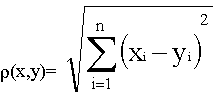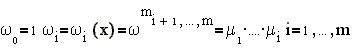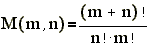Равномерные приближения

            Пусть в области     D Ì Rⁿ         задана непрерывная функция многих переменных (ф.м.п.),  f(x), x=(x₁, ... , x_n)      принимающая на заданном множестве    M   точек   x_i  Ì D  соответственно значения   f(x_i), i=0,...,k .  Рассмотрим задачу численного построения функции   p(x),   принимающей в заданных точках множества заданные значения  f(x_i),  а в остальных точках области   D Ì Rⁿ    изображающую функцию точно или приближенно.
            Будем искать решение поставленной задачи в виде метрических многочленов.
Будем рассматривать n-мерное пространство   Rⁿ   как Евклидовое с метрикой 

В качестве отношения частичного порядка   ≤ в n-мерном пространстве   Rⁿ выберем естественное отношение порядка, т.е.,    

                                       x ≤ y, Û x_i ≤ y_i ,        i=1, ... n.         

Определим в пространстве    Rⁿ    функцию     sign(x)    вида

                                                                      1, x>0,
                                          sign(x) = {  0,x=0,
                                                            -1, x<0

Выберем в пространстве     Rⁿ   m    произвольных точек       c_i , i=1,...,m  таких, что для любого  x Ì  D    имеет место   x ≤ c_i   или  c_i  ≤ x  . Функция вида

m_i  =m _x(x,c_i) = sign(x-c_i)*r (x,c_i).

называется полуупорядоченной метрикой в Rⁿ . Тогда функции вида

будем называть базисными метрическими функциями (б.м.ф.).  
Здесь  (m)_i+1,...,m  -     мультииндекс, (m)_i+1,...,m=(1,...,i).  Нижние индексы обозначают отсутствующие номера в последовательности (1,...,m).   
           Многочлены вида

                        p_m(x)= a_{0 *} w₀(x)+ a_1* w₁(x) + .... +a_m* w_m(x) ( 1 )

где    a₀, a₁ ..., a_m  Ì  R¹ , w₀(x) , w₁(x) .... , w_m(x) построенные по системе б.м.ф., называются метрическими многочленами (м.м.). Эти многочлены будем использовать для приближения тестовых функций   f(x).
          Будем полагать, что ф.м.п. f(x) задана на множестве точек, находящихся в произвольном положении. Для построения приближений используем множество M, содержащее 12 точек. Для оценки качества приближения используем другое множество N, содержащее 10 контрольных точек. Контрольные точки множества  N находятся между точками множества M. .Пример выборки точек для n=3 представлены на рис.1,2.

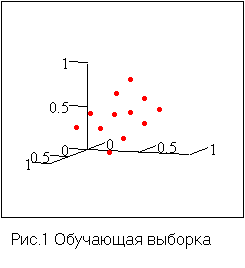
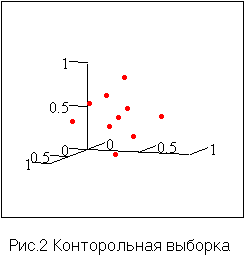
Из рис.1, рис.2 видно, что точки не образуют какую-либо специально подобранную конфигурацию, обеспечивающую хорошее приближение. 
           Данная задача является задачей не только построения приближения в заданных точках многомерного пространства, но и задачей прогнозирования временных рядов x(t), т.е. задачей построения приближенной зависимости вида

x_t+1=f(x_t,x_t-1,...,x_t-s)=f(X)

где X=(x_t,x_t-1,...,x_t-s) является прямой суммой значений   x_t,x_t-1,...,x_t-s   временного ряда в точках t,t-1,...,t-s.  Так, исходные данные для задачи прогнозирования одномерного временного ряда   x(t)  вида

x_t+1=f(x_t,x_t-1,x_t-2)=f(X)

будут образовывать в трехмерном пространстве множества, аналогичные множествам изображенным на рис. 1,2. 
           Число переменных     n.    каждой из приближаемых функций равно n=2^p, 
p = 1, ... , 12. Степень m   м.м. изменялась от 2 до 10.   Точность приближения функций оценивается по средней относительной погрешности в процентах, вычисленной в точках обучающей и контрольной выборки.
           В таблицах приведены результаты  построения приближений для 
функции y1,  функции y2,  функции y3,  функции y4,  функции y5,  функции y6.
           Получены следующие результаты.
1.. Обнаружена сходимость м.м при увеличении степени приближающего м.м. Для разных функций скорость сходимости различна, что объясняется различием их дифференциально-разностных свойств.
2. Обнаружена сходимость м.м. к исходной ф.м.п. при увеличении числа переменных ф.м.п. при неизменной степени м.м. Это новый тип сходимости приближений ф.м.п. Для разных ф.м.п. скорость сходимости различна, что объясняется различием их дифференциально-разностных свойств.
3. Численно обнаружено влияние количества переменных функции на скорость  сходимости м.м. С ростом количества переменных скорость сходимости м.м. увеличивается.
   Полученные результаты позволяют сделать следующие выводы.
1. М.м. представляют собой эффективный аппарат для численного построения приближения ф.м.п.
2. Формулы для приближения ф.м.п. м.м. аналогичны формулам для приближения функций одного переменного, что делает удобным использование м.м. в теоретическом анализе.
3. Формулы для приближения ф.м.п. м.м. намного проще формул для приближения алгебраическими многочленами многих переменных. Число коэффициентов алгебраического многочлена n переменных степени m равно

При m=10 и n=4096

M(m,n)=371247092490302324724109827585>3.7*10²⁹

Число коэффициентов м.м. при m=10  и   n=4096  равно 11. Таким образом, использование м.м. для приближения ф.м.п. во много раз уменьшает количество вычислений и объем памяти компьютера, необходимых для построения приближения ф.м.п. Это позволяет осуществлять практическое построение м.м., содержащих сотни и тысячи переменных, без использования очень мощных компьютеров.
4. Приближения ф.м.п. м.м. требуют намного меньше исходных данных для численного построения м.м., чем приближения посредством алгебраических многочленов многих переменных. Так, для приближения функций от 4096 переменных алгебраическими многочленами степени 10 потребовалось бы более   3.7*10²⁹     точек. При приближении м.м. степени 10 использовалось 12 точек. Тем самым обеспечивается возможность построения моделей больших, многомерных социально-экономических, экологических, биологических и технических объектов, для которых получение большого количества экспериментальных данных затруднено, связано с большими материальными затратами, требует длительного времени или невозможно.
5. Использование м.м. для построения приближенных зависимостей снимает проблему устранения взаимной зависимости переменных, так как все переменные используются совместно. Но именно такой подход и соответствует реальности. В сложных системах, описываемых большим количеством параметров, все параметры обычно изменяются одновременно.