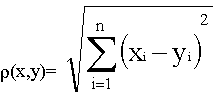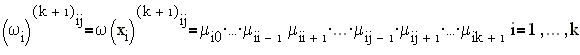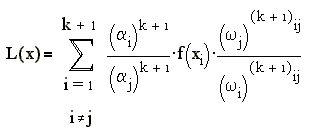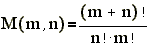|
Пусть
в области D Ì
Rn
задана непрерывная функция
многих переменных (ф.м.п.)
f(x), x=(x1, ... , xn)
принимающая на заданном множестве
M
точек xi
Ì
D соответственно
значения
f(xi),
i=0,...,k .
Рассмотрим задачу численного
построения функции
p(x), принимающей в
заданных точках множества заданные
значения f(xi),
а в остальных точках области D
Ì Rn ,
располагающихся между заданными
точками, изображающую функцию точно или
приближенно.
Будем искать
решение поставленной задачи в виде
интерполяционных метрических
многочленов Лагранжа (и.м.м.Л).
Будем
рассматривать n-мерное пространство
Rn
как Евклидовое с метрикой
|
|
В качестве отношения частичного
порядка ≤
в n-мерном
пространстве Rn
выберем
естественное отношение порядка, т.е.,
x ≤
y, Û xi ≤
yi , i=1, ... n.
Определим
в пространстве Rn
функцию sign(x)
вида
1, x>0,
sign(x) = { 0,x=0,
-1, x<0
Тогда полуупорядоченной
метрикой в Rn
будет метрика
вида
m =m
x(x,y
) = sign(x-y)*r
(x,y).
Эта
функция определена
только
для тех
x,y,
которые удовлетворяют
условию
x
≤ y
или y ≤
x.
Тогда
mij = m
x(xi,xj
)
Полагаем, что
множество точек интерполирования и
интерполируемая точка
x
образуют
упорядоченную последовательность вида
x0<=...<=x<=...<=xk
( 1 )
|
|
Пусть
в последовательности ( 1 )
интерполируемая точка x
имеет порядковый номер j. Тогда
последовательность ( 1 ) может быть
переписана в виде
x0<=...<=xj<=...<=xk+1
(
2 )
Для последовательности ( 2 ) определим
мультииндексы вида
(k+1)=(0,...,k+1), (k+1)0=(1,...,k+1),
(k+1)k+1=(0,...,k),
(k+1)ij=(0,1,...,i-1,i+1,...,j-1,j+1,...,k+1)
где нижний индекс обозначает
отсутствующий номер в
последовательности (0,1....,k,k+1).
Функция вида
|
|
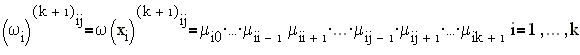
|
называется базисный
метрический функционал (б.м.ф.).
Многочлен
вида
|
|
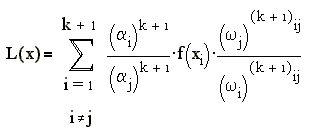
|
|
где
|
|

|
|
называется интерполяционный
метрический многочлен Лагранжа (и.м.м.Л.).
Козффициенты (ai)k+1
вычисляются следующим образом.
Вычисление коэффициентов начинается с
вычисления коэффициентов для
последовательности точек x0,
x1, x2. Затем
вычисляются коэффициенты для
последовательности x0,
x1, x2 , x3 .
Для этого сначала вычисляют
коэффициенты для
подпоследовательности x0,
x1, x2 и подпоследовательности
x1, x2 , x3
. После этого вычисляются коэффициенты
для всей последовательности x0,
x1, x2 , x3 .
Аналогичным образом вычисляются
коэффициенты для
последовательности x0, x1, x2 , x3
, x3.
Будем полагать, что ф.м.п. f(x) задана
на множестве точек,
находящихся в произвольном
положении. Для построения
приближений используем
множество M,
содержащее 10 точек. .
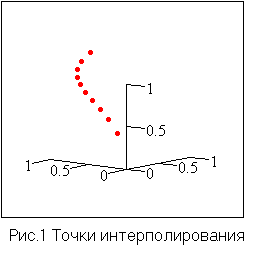
Пример
выборки точек для
n=3 представлены на
рис.1.
|
|
|
|
Из рис.1 видно, что точки
интерполирования не образуют
регулярную сетку точек и не
принадлежат прямой линии.
Число переменных
каждой из приближаемых функций
принималось равным n=2p
, p = 1
... , 10. Степень и.м.м.Л.
изменялась от 1 до 8.
Количество точек, используемых для
построения приближения, изменялось от 2
до 9. В качестве тестовых точек
использовались промежуточные точки множества, не
использованные для построения
приближения. Точность приближения
оценивалась по средней относительной
погрешности приближения
функций в процентах в точках, которые
располагаются между первой и последней
точкой в последовательности точек,
используемых для интерполирования.
В таблицах
приведены результаты
вычислений для функции
y1, функции
y2,
функции
y3, функции
y4, функции
y5, функции
y6.
В результате построения
интерполяционных метрических приближений
ф.м.п. получены следующие результаты.
1. Обнаружена сходимость и.м.м.Л. к
исходной ф.м.п. при увеличении степени и.м.м.Л.
Для разных ф.м.п. скорость сходимости
различна, что объясняется различием их
дифференциально-разностных свойств.
2. Обнаружена сходимость и.м.м.Л. к
исходной ф.м.п. при увеличении числа
переменных ф.м.п. при неизменной
степени и.м.м.Л. Это новый тип
сходимости приближений ф.м.п. Для
разных ф.м.п. скорость сходимости
различна, что объясняется различием их
дифференциально- разностных свойств.
3. Численно обнаружено влияние
количества переменных ф.м.п. на
сходимость и.м.м.Л. С ростом количества
переменных ф.м.п. скорость сходимости
увеличивается.
Полученные результаты позволяют
сделать следующие выводы.
1. И.м.м.Л. представляют собой
эффективный аппарат для численного
построения приближения ф.м.п.
2. Формулы для интерполирования ф.м.п. и.м.м.Л.
аналогичны формулам для
интерполирования функций одного
переменного, что делает удобным
использование и.м.м.Л. в теоретическом
анализе.
3. Формулы для интерполирования ф.м.п. и.м.м.Л
намного проще формул для
интерполирования алгебраическими
многочленами многих переменных. Число
коэффициентов M(m.n)
алгебраического
многочлена
n
переменных степени m
равно
|
|
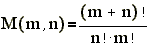
|
|
При n=1024 и m=8
M(m,n)=31053118674088663425>3*1019
Число коэффициентов и.м.м.Л. при
n=1024 и m=8
равно
9. Таким образом, использование и.м.м.Л.
для интерполирования ф.м.п. во много раз
уменьшает количество вычислений и
объем памяти компьютера, необходимых
для построения приближения ф.м.п. Это
позволяет осуществлять практическое
построение и.м.м.Л., содержащих сотни и
тысячи переменных, без использования
очень мощных компьютеров.
4. Использование и.м.м.Л. не требует
построения регулярной сетки
интерполяционных точек. Это во много
раз уменьшает количество исходных,
необходимых для численного построения
и.м.м.Л. по сравнению с приближением
посредством алгебраических
многочленов многих переменных. Так, для
интерполирования функций от 1024
переменных алгебраическими
многочленами многих переменных
потребовалось минимум 21024
точек для
построения регулярной сетки точек. При
интерполировании и.м.м.Л. для
построения упорядоченной
последовательности точек
использовалось не более 9 точек. Это
открывает возможность построения
моделей больших, многомерных социально-экономических,
экологических, биологических и
технических объектов, для которых
получение большого количества
экспериментальных данных затруднено,
связано с большими материальными
затратами, требует длительного времени
или невозможно.
5. Так как для приближения ф.м.п.
посредством и.м.м.Л. не требуется
построение регулярной сетки точек, то
использование и.м.м.Л упрощает и
расширяет возможность использования
экспериментальных данных.
Экспериментальные точки должны быть
лишь упорядочены в заданном отношении
порядка.
|