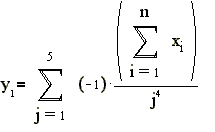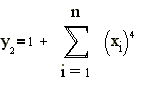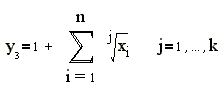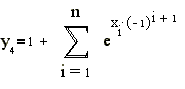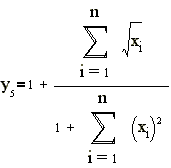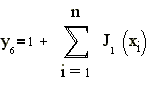Численное исследование метода моделирования

Большие системы
Математическое описание большой системы 
Метрический анализ

Задачи численного исследования 
Равномерные приближения
Интерполяционные приближения

Задачи численного исследования

Численное исследование метрических приближений имеет своей целью определение возможности и эффективности использования метрических приближения для построения приближенных моделей больших систем.

Здесь необходимо сказать несколько слов о том, насколько результаты, полученные при решении тестовых задач, дают представление о возможностях строить модели больших систем  с помощью данного численного метода. 

Любой численный метод представляет собой некоторый алгоритм вычислений и, в конечном счете, некоторую компьютерную программу для обработки числовой информации, некоторого набора чисел.

В компьютере не существует числовой клавиатуры, соответствующих регистров процессора и программ обработки для "нереальных" тестовых чисел и для “реальных” чисел. В компьютере существует единая система для работы с числами. Способ получения чисел и для алгоритма, и для компьютера не имеет значения и никак не учитывается. 

Таким образом, для численного метода не существует двух видов исходных данных: “нереальных”, тестовых данных и “реальных”, экспериментальных данных. 

Однако между тем или иным набором и тестовых, и экспериментальных данных для численного метода все же существует различие и заключается оно в следующем.

Между числовыми данными, используемыми численным методом, существуют те или иные математические зависимости. Для тестовых исходных данных эти зависимости могут задаваться в виде математических формул. Фактически, тестовые исходные данные часто и и генерируются с помощью заранее выбранных математических формул. Для экспериментально полученных исходных данных эти зависимости определяются неявно объективно существующими в мире закономерностями.

Для численного метода различие между наборами исходных данных заключается в сложности зависимостей между этими исходными данными. Чем сложнее зависимость между исходными данными, тем более трудоемким становится решение задачи, которое определяется количеством исходных данных и количеством вычислений, необходимых для реализации численного метода.

Любой численный метод предназначен для решения не одной, а целого класса задач. Эти задачи могут отличаться разным видом и уровнем сложности зависимостей между параметрами задачи. Поэтому тестирование численного метода заключается в решении  целого набора тестовых задач. Сложность тестовых зависимостей должна строится исходя из сложности зависимостей в конкретной проблемной области. Тогда  зависимости между параметрами реальной задачи будут по типу и уровню сложности соответствовать одной из уже решенных тестовых задач. В этом случае после решения тестовых задач можно быть уверенным, что данный численный метод справиться и с реальной задачей.

Таким образом, проверка численного метода на наборе тестовых задач есть решение целого класса реальных задач. Безусловно, что при решении реальных задач и алгоритм, и программа должны “доводится” в соответствии с требованиями реальной задачи.

Будем полагать, что функция многих переменных (ф.м.п.)  f(x), x=(x₁, ... , x_n)  определена в n-мерной области   DÌ Rⁿ ,   задаваемой соотношениями   

                                       0 <=x_i <= 1 ,            i=1, ... n.  
Значения функции    f(x)   известно в k точках области D.

В качестве приближаемых будем использовать следующие функции:

    где  J1(x)- Бесселевы функции первого рода.

Для каждой приближаемой функции строились интерполяционные и равномерные метрические приближения. При этом исследовались следующие зависимости.
1. Сходимость метрических приближений при увеличении степени приближающего метрического многочлена.
2. Влияние числа переменных на сходимость метрических приближений.